Introducing the `k256` crate: a pure Rust secp256k1 library based on projective formulas

By Tony Arcieri

The Rust programming language has received widespread adoption in the cryptocurrency space, owing to many things like its emphasis on safety, sophisticated type system, and impressive support for concurrency and async I/O. However, where Rust has succeeded in this space, it’s been despite the language’s sometimes spotty support for cryptographic algorithms used in cryptocurrency development.

One of the most critical algorithms commonly used in cryptocurrency is elliptic curve cryptography (ECC). While there are many impressively high quality ECC implementations written from the ground up in pure Rust, such as the curve25519-dalek and bls12_381 crates, the story around the most commonly used elliptic curve in cryptocurrency, secp256k1, is a bit more confusing and fragmented.

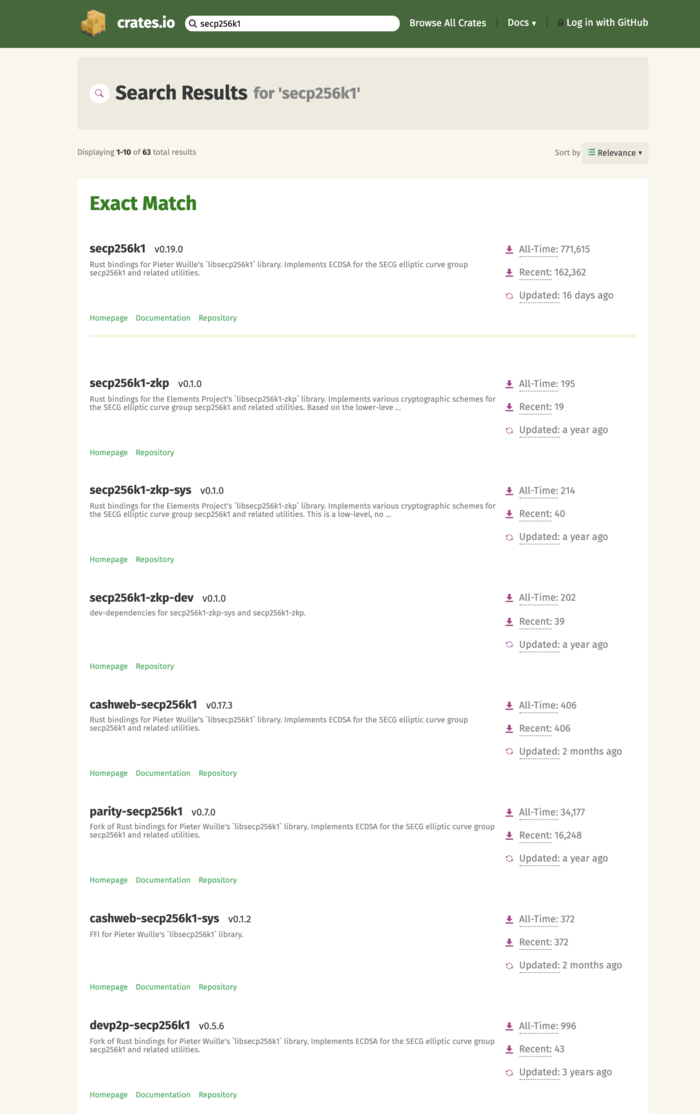
Here is a screenshot of the results you get if you search for “secp256k1” on crates.io, the Rust package repository:

The common theme here: lots and lots and lots of forks of Rust bindings to the bitcoin-core/secp256k1 C library. Using this library certainly isn’t a bad choice: it’s the fastest, most mature, and best-maintained secp256k1 library available. However, people are writing forks because the Rust bindings do not provide access to the C library’s API surface necessary to implement things like zero-knowledge protocols.

All that said, while Rust has fantastic C interop support, for many reasons it’s much nicer to have a high-quality pure Rust library over a C library. Concerns about the C language like memory safety aside, using C libraries limits portability because you also need a C compiler installed for all of your potential targets. It often slows down builds by requiring a build.rs step (as in secp256k1-sys which packages the bitcoin-core/secp256k1 library). When available, it’s much more convenient to use a high-quality Rust library than a C library wrapper.

There has been one attempt (to our knowledge) to create a pure Rust secp256k1 implementation: the paritytech/libsecp256k1 library released as the libsecp256k1 crate. However, this library is problematic for a few reasons:

• It implements incomplete elliptic curve formulas based on Jacobian coordinates. These were, for awhile, the state-of-the-art, but still lead to a number of security vulnerabilities in practice owing to their incompleteness and difficulty to implement in constant-time. While 2014 saw the discovery of pseudo-complete Jacobian addition formulas, they were for the most part obsoleted in 2015 by the discovery of efficient and complete addition formulas for prime order elliptic curves based on projective coordinates, which are also straightforward to implement in constant-time using techniques similar to the Montgomery ladder commonly used to implement Curve25519. The k256 crate implements the new projective formulas, which per the aforementioned paper aim to achieve a sweet spot in the tradeoffs between “simplicity, security, and speed”.
• libsecp256k doesn’t expose elliptic curve arithmetic as part of its public API, which is needed to implement things like zero-knowledge protocols, and as illustrated in the screenshot of crates.io above has lead to a proliferation of forks instead. Furthermore, it’s probably best that it doesn’t, as misusing arithmetic based on the Jacobian formulas could lead to potential security vulnerabilities.
• The approach to “constant time” code libsecp256k1 uses is somewhat questionable. For comparison, the k256 crate uses idiomatic patterns for implementing constant-time code in conjunction with the subtle crate, which lower to simple, efficient machine code.
• libsecp256k1 appears to be a translation from C code, or at least follows C-like idioms which seem very low-level for a Rust library. While mechanically translating a high-quality C library might be a good starting point for a Rust library, it doesn’t feel like sufficient effort been applied to remove C-isms from the codebase.

Introducing the k256 crate #

• GitHub: https://github.com/RustCrypto/elliptic-curves/tree/master/k256
• Crates.io: https://crates.io/crates/k256
• Docs: https://docs.rs/k256/

The k256 crate is a pure Rust secp256k1 implementation created as part of the RustCrypto/elliptic-curves project. It’s the work of many collaborators who are interested in improving the quality of elliptic curve cryptography within the Rust ecosystem as well as specifically producing a high-quality secp256k1 library.

The project began as a fork of the RustCrypto p256 crate, which implements the NIST P-256 curve and was originally written from scratch by Jack Grigg (a.k.a. str4d), cryptographer, Zcash engineer, and co-author of several other elliptic curve libraries including the bls12_381 crate.

It was forked into the k256 crate by “tux” of NuCypher. Both NIST P-256 and secp256k1 are similar in that they are short Weierstrass curves, making it possible to repurpose large parts of the implementation for a different curve, namely reusing the Montgomery arithmetic code but despecializing it from the P-256 modulus.

Thanks to significant contributions by another NuCypher employee, Bogdan Opanchuk, the k256 crate now has both 32-bit and 64-bit backends leveraging several techniques used by the bitcoin-core/secp256k1, including lazy reduction and endomorphism optimizations. The latter were previously patented, but the last remaining patent recently expired allowing us to enable the endomorphism optimizations by default and remove the non-endomorphism code.

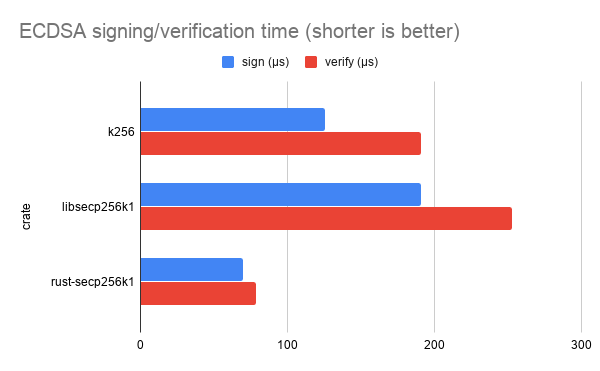
Below is a benchmark comparing the ECDSA signing and verification performance of the k256 crate, the pure Rust libsecp256k crate, and the C FFI (rust-)secp256k1 crate which wraps the bitcoin-core/secp256k1 library respectively:

The bitcoin-core/secp256k1 C library provides the best performance, but the k256 crate is not substantially slower: it’s ~1.8x slower at signing, and ~2.4x slower at verification, as benchmarked on an Intel® Xeon® E-2286M CPU @ 2.40GHz.

Tour of the k256 API #

As mentioned above, the k256 crate is a general-purpose secp256k1 library. It’s implemented without heap allocations and designed from the ground-up to work in no_std environments.

It comes with the following features out-of-the-box:

ECDSA #

The Elliptic Curve Digital Signature Algorithm is one of the most common algorithms used in conjunction with the secp256k1 elliptic curve. As illustrated by the chart above, it’s also one of the main algorithms we’ve focused on in developing the k256 crate.

In k256, we’ve implemented ECDSA by leveraging shared functionality exposed from the ecdsa crate, which is generic over elliptic curves. The ecdsa crate implements functionality like RFC6979 deterministic signatures, including a mode of RFC6979 which takes additional randomness from an RNG, which can be used to harden it against things like fault attacks on embedded devices.

Additionally, the k256 crate supports Ethereum-style signatures with public key recovery, which are generic over digest functions and can be used in conjunction with Keccak256 as used by Ethereum.

In developing the k256 crate, we’ve definitely had cryptocurrency use cases on the top of our minds. If there’s some cryptocurrency application where you’d like to use secp256k1 and it’s not supported by the k256 crate, please open an issue!

Elliptic Curve Diffie-Hellman #

Diffie-Hellman key exchange is the primary way to perform public-key encryption using elliptic curves, and the k256 crate supports it.

It uses a shared, generic Diffie-Hellman implementation from the elliptic-curve crate.

Group-based operations #

The k256 crate provides support for implementing any group-based protocol using the Scalar, AffinePoint, and ProjectivePoint types. These types implement traits from the ff (i.e. finite field) and group crates. Most notably ProjectivePoint implements the group::Group trait, and with it a whole host of arithmetic operations such as point addition and scalar multiplication.

As mentioned at the beginning of this post, by making group-based operations part of the public API, it’s not necessary to fork the k256 crate in order to implement e.g. zero-knowledge protocols.

The idea of exposing “internals” of a cryptographic library like this may sound scary, however we have meticulously designed a safe API which is hard-to-misuse. When working with complete formulas for prime order curves like k256 implements, properly encapsulated in types which do not allow misuses by design, groups naturally lend themselves to safe APIs.

That’s not to say that group-based protocols are easy, or that k256 will somehow save you from a protocol-level design error. However, if you’re doing something like implementing a well-scrutinized group-based protocol with a security proof from a paper, k256 should make it easy to translate the prose in a paper into Rust code while avoiding implementer error (ideally catching mistakes with the help of Rust’s type system).

Crates using k256 today #

Though we haven’t done any sort of marketing push around it yet, the k256 crate has seen quite a bit of organic adoption. Here are a list of some of the notable crates using k256 today:

• enr: an implementation of an Ethereum Node Record as specified by EIP-778.
• ethers-rs: complete implementation of Ethereum and Celo wallets in Rust.
• jwt-simple: lightweight security-oriented implementation of JSON Web Tokens
• stdtx implementation of the Cosmos StdTx format, developed by us here at iqlusion.
• tendermint-rs: implementation of the Tendermint high-performance blockchain consensus engine being developed in Rust by Informal Systems

Conclusion #

If you’re using secp256k1 and want a pure Rust implementation of the elliptic curve, or just access to group-based operations as part fo the public API, give k256 a try!

If you’re having any trouble using it, please open a GitHub issue on our issue tracker, or say “hi” in our Zulip Chat.